# Recursions

# Recursive v.s. Iterative

遞迴 v.s. 迭代

關於遞迴與迭代解決問題的方式：

遞迴：透過重複將問題分解為同類的子問題，而解決問題的方法。通過 呼叫函式本身 來進行
迭代：其目的通常是為了接近所需求的目標或結果。每一次對過程的重複被稱為一次迭代，每一次迭代得到的結果通常會被用來作為下一次迭代的初始值

# 以費氏定理為範例

費氏定理 - 前兩數的相加，為第三數的和

首幾個 Fibonacci 數是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

遞迴解法，使用 call stack 代替 for loop，用 return 形式追蹤每次呼叫的狀態

function factorial(n) {
  if (n <= 1) return n;
  return factorial(n - 2) + factorial(n - 1);
}

1
2
3
4

迭代解法，使用可變的狀態作為計數器

function factorial(n) {
  var start = 0;
  var end = 1;
  var result;

  if (n <= 1) {
    return n;
  } else {
    for (let i = 2; i <= n; i++) {
      result = start + end;
      start = end;
      end = result;
    }
    return result;
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# binary tree

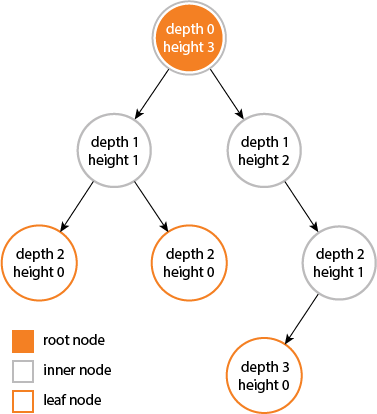
binaryTree

上圖的最大深度為 3。

使用遞迴的解法，當找不到節點時，深度為 0，

如果節點有左或右的子節點時，則比較左和右子節點的深度，取最大值，

那麼當前的深度會是 最大子樹深度 + 1。

const node = {
  left: {
    left: {},
    right: {},
  },
  right: {
    right: {
      left: {},
    },
  },
};

const maxDepth = (node) => {
  if (!node) return 0;
  const depthLeft = maxDepth(node.left);
  const depthRight = maxDepth(node.right);

  return 1 + Math.max(depthLeft, depthRight);
};

maxDepth(node) - 1; // 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# Tail Calls 尾調用

概念：一個函式的在最後一步是 call 另外一個函式，並 不保留 目前函式的狀態。

以 func1 -> func2 -> func3 為例，當 call func2 的動作在 func1 的對底部執行，那 func1 的 stack frame 就不需要了，也叫表示記憶體可以釋出(因為 func1 做完了)。

如果 Tail Call 自己，又稱為 tail-recursive 尾遞迴，這時候只會存在一個 stack frame，所以理論上遞迴 stack 可以一直運算下去。

# Tail Call Optimizations (TCO) 尾調用優化

TCO 是使得 Tail Call 更高效運行的優化，要做到 TCO，必須正確書寫 Tail Call。

正確書寫 Tail Call 的技巧稱作 PTC (Proper Tail Calls，正確的尾調用)。

# 不正確 PTC

function factorial(n) {
  if (n === 0) {
    return 1;
  }
  return n * factorial(n - 1);
}

1
2
3
4
5
6

因為 factorial(n - 1) 執行後，n * 才會執行，記憶體最多需要保存 n 個 stack frame。

# 正確 PTC

function factorial(n, partialFactorial = 1) {
  if (n === 0) {
    return partialFactorial;
  }
  return factorial(n - 1, n * partialFactorial);
}

factorial(5); // 120

1
2
3
4
5
6
7
8

同時記憶體只需要保存一個 stack frame。

# 常見的不正確 PTC

// 函式的在最後一步需 call 另外一個函式
foo( .. );
return;

// 同上
var x = foo( .. );
return x;

// 記憶體會保存 n 個 stack frame
return 1 + foo( .. );

1
2
3
4
5
6
7
8
9
10

# Continuation-passing style

不是所有的遞迴都可以按照 PTC 規範重構（Proper Tail Calls），如多重遞迴（multiple recursion），或者是交互遞迴（mutual recursion），這些是函式內，呼叫多次遞迴，這些都很難做到 PTC 得到優化（因為沒有辦法把多個遞迴放到最後）。

Continuation 表示函式結束後，把要做的事指定給下一個函式 (當作參數)。

以加總為例：

const sumRecursion = (function() {
  const recursion = ([result, ...nums], fn) => {
    if (!nums.length) return fn(result);
    return recursion(nums, (x) => fn(result + x));
  };
  return (...nums) => recursion(nums, (x) => x);
})();

sumRecursion(1, 2, 3); // 6

1
2
3
4
5
6
7
8
9

CPS 中每個函數都有一個額外的參數 (fn) 用来表示當一個函數執行完畢該做什麼。

當遞迴到最後一個 3 ，滿足基本的條件時，才開始執行 fn，注意是到最後才執行 fn。這邊是遞迴的邏輯：滿足基本條件，一層層逐步返回部分結果。

所以，在最後一個步驟會得到一個很深的巢狀函數：

fn(1 + fn(2 + fn(3)))

# PTC 和 CPS 的比較

	執行方式
PTC	把部分結果傳遞給下一個遞迴
CPS	將運算步驟閉包在一個 continuation callback 函數中，並延遲 (defer) 到最後一步才開始執行

PTC 和 CPS 皆滿足 TCO，因為當前的遞迴執行結束後，就不需要再回來，所以可以將 stack frame 移走，避免堆疊更多 stack frame。

# 參考

Recursion 遞迴 (opens new window)

Tail Calls 尾調用 (opens new window)

Continuation-passing style (opens new window)

← Pure Function pipe 和 compose →